What is Category Theory?
This section explains the foundational concepts of category theory, such as functors, morphisms, and natural transformations, and their applications in both mathematics and economics. It links these ideas to the Lucas critique and explores their role in econometric duality.
:::info Author:
(1) David Staines.
:::
Table of Links
4 Calvo Framework and 4.1 Household’s Problem
4.3 Household Equilibrium Conditions
4.5 Nominal Equilibrium Conditions
4.6 Real Equilibrium Conditions and 4.7 Shocks
5.2 Persistence and Policy Puzzles
6 Stochastic Equilibrium and 6.1 Ergodic Theory and Random Dynamical Systems
7 General Linearized Phillips Curve
8 Existence Results and 8.1 Main Results
9.2 Algebraic Aspects (I) Singularities and Covers
9.3 Algebraic Aspects (II) Homology
9.4 Algebraic Aspects (III) Schemes
9.5 Wider Economic Interpretations
10 Econometric and Theoretical Implications and 10.1 Identification and Trade-offs
10.4 Microeconomic Interpretation
\ Appendices
A Proof of Theorem 2 and A.1 Proof of Part (i)
B Proofs from Section 4 and B.1 Individual Product Demand (4.2)
B.2 Flexible Price Equilibrium and ZINSS (4.4)
B.4 Cost Minimization (4.6) and (10.4)
C Proofs from Section 5, and C.1 Puzzles, Policy and Persistence
D Stochastic Equilibrium and D.1 Non-Stochastic Equilibrium
D.2 Profits and Long-Run Growth
E Slopes and Eigenvalues and E.1 Slope Coefficients
E.4 Rouche’s Theorem Conditions
F Abstract Algebra and F.1 Homology Groups
F.4 Marginal Costs and Inflation
G Further Keynesian Models and G.1 Taylor Pricing
G.3 Unconventional Policy Settings
H Empirical Robustness and H.1 Parameter Selection
I Additional Evidence and I.1 Other Structural Parameters
I.3 Trend Inflation Volatility
F.2 Basic Categories
This part helps with understanding the concepts underpinning Definition 13. It also develops the theory behind Figure 1 in Section 9 and draws links with other items in this appendix. Category theory uses formal diagrams to study underlying mathematical relations. A Category is a labelled directed graph whose nodes are called Objects and labelled directed edges are called morphisms or Arrows. Categories have two basic properties: arrows can be composed associatively and for every object there is an identity map. Vakil [18 October, 2017] has an excellent chapter expositing category theory, with a view to algebraic geometry. Leinster [2014] is a general introduction.
\ F.2.1 Discussion and Examples
\ Categories represent abstractions of other mathematical concepts. Many familiar concepts and structures can be viewed as categories. It simplifies the process of stating and proving theorems and helps with understanding similarities between seemingly disparate areas of mathematics.
\ Perhaps the most basic example of a category is the category of sets, where the objects are sets and the arrows represents functions between these sets. The strength of the framework is that any system, that can be built from associative mappings, can be analyzed in this way. Arrows are often said to represent Structure-Preserving Transformations between objects.
\ This is most apparent with the family of concrete categories, informally, those that can be viewed as part of the category of sets but with additional restrictions on the arrows. First is Top, whose objects are topological spaces with continuous functions as morphisms. From basic analysis and topology these preserve compactness, connectedness and separability properties. In differential topology the category Smooth has smooth manifolds as objects and maps that preserve this property (smooth maps) as arrows. In Homotopy maps preserve homotopy between pointed topological spaces.
\ The insight is more general. The class Grp consists of groups and homomorphisms that retain the group structure of the object in the target. Categories have their own structure-preserving processes called Functor.
\ A functor associates to every object in one category an object in another and every morphism one in the other. Categories allow for significant abstraction, for instance, it is possible to define the category of Categories and Functors with categories as objects and functors as arrows. Finally, Natural Transformations are mappings between functors that obey certain commutativity conditions. Functors and natural transformations underpin the "diagram chasing" method, exemplified in Figure 1 in the text.
\ F.2.2 Categories and Morphisms
\ A category C comprises the following three mathematical entities
\ • A family ob(C), whose elements are called objects.
\ • A class hom(C), whose elements are known as morphisms, maps or arrows. f : a → b denotes a morphism from source a to target b.
\ • hom(a, b) denotes the hom-class of all morphisms from a to b, for example, all the smooth functions between sets a and b in Smooth.
\ • A binary operation ◦, called composition of morphisms, such that for any three objects a, b and c ◦ : hom(a, b) × hom(b, c) → hom(a, c). The composition of f : a → b with g : b → c rendered g ◦ f or gf is governed by two familiar axioms
\ i Associativity: If f : a → b, g : b → c and h : c → d then h◦(g◦f) = (h◦g)◦f
\ ii Identity: For every object x, there exists a morphism 1x : x → x, called the identity morphism, such that for every morphism f : a → b, it is the case that 1b ◦ f = f ◦ 1a
\ Intuitively, the first condition is essential to define paths around diagrams. It is common to notions of multiplication and addition. The second, is a requirement that no matter how layered the algebraic structure, one can drill down to the primitive level typically points, sets or maps.
\ Relations between morphisms, like fg = h, are often depicted in commutative diagrams, with vertices representing objects and arrows representing morphism. A morphism f : a → b can possess the following properties:
\ • Monomorphism (or monic) if f ◦ g1 = f ◦ g2 implies g1 = g2, for all morphisms g1, g2 : x → a
\ • Epimorphism (or epic) if g1 ◦ f = g2 ◦ f for any g1, g2 : b → x
\ • Bimorphism if f is both monic and epic
\ • An Isomorphism if there is another morphism g : b → a where f ◦ g = 1b and g ◦ f = 1a
\ A category is Abelian if it has the subsequent attributes:
\ • It is pre-additive, so for any three morphisms f, g and h and the group operator +
\ f ◦ (g + h) = f ◦ g + f ◦ h
(f + g) ◦ h = f ◦ h + g ◦ h
\ Thus every set Hom(a, b) has an abelian group structure and function composition is distributive over the group operator.
\ • It has a zero object I, such that for any other object Z, the object is initial, so there is exactly one morphism I → Z and final, in the sense that there is only one mapping Z → I.
\
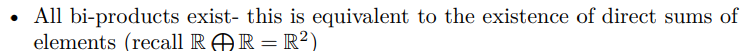
\ • It has all kernels and cokernels.
\ • All morphisms and epimorphisms are normal.This means the category behaves as though there is a set which is the destination for all mappings.
\ • An object F(x) in D for any object x in C and
\ • A morphism F(f) : F(x) → F(y) for each morphism f : x → y in C
\ with the properties that
\
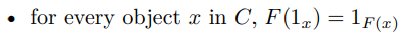
\ • all morphisms compose associatively so f : x → y and g : y → z imply F(g ◦ f) = F(g) ◦ F(f)
\ A Contravariant functor F : C → D behaves like a covariant functor, except with all the morphisms turned around. More specifically, every morphism f : x → y in C is assigned to a morphism F(f) : F(y) → F(x) in D. Equivalently, a contravariant functor acts as a covariant functor from the opposite category C op to D, where the opposite category C op is C with all its arrows reversed
\ Formally, a Natural Transformation is a relation between two functors. Functors often describe so called natural constructions and natural transformations represent natural homomorphisms between these constructions. When two different constructions yield the same result an isomorphism arises between the two functors.
\ If F and G are covariant functors between the categories C and D, then a natural transformation η from F to G associates with every object x in C a morphism ηx : F(x) → G(x) in D, such that for every morphism f : x → y, the relationship ηy ◦ F(f) = G(f) ◦ ηx. Thus, I construct a commuting diagram below. The two functors F and G are referred to as naturally isomorphic because there exists a natural transformation from F to G, such that ηx is an isomorphism for every x in C.
\
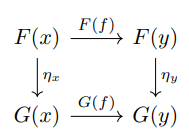
\ Next I can define a Concrete Category as a pair (C, U), such that C is a category, and U : C → Set (the category of sets and functions) is a faithful functor- one which is one-to-one when restricted to morphisms with the same target and source. The functor U is to be thought of as a so called forgetful functor, which assigns to every object of C its "underlying set", and to every morphism in C its "underlying function". Thus a concrete category can be viewed as the category of sets but with a restriction on the set of possible morphisms, like differentiability or requiring uniform continuity (often denoted Uni).
\ An Exact Functor is one which preserves short exact sequences (those that end in zero after three or fewer steps). Formally, let P and Q be abelian categories, and let F : P → Q be a covariant additive functor (so that, in particular, F(0) = 0). We say that F is an exact functor if, whenever
\
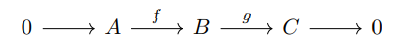
\ is a short exact sequence in P, then
\
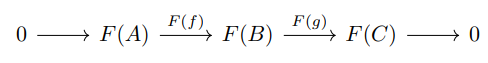
\ is a short exact sequence in Q. It is often easier to work with the weaker notion of a Left Exact sequence defined below
\
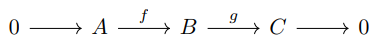
\ is a short exact sequence in P, then
\
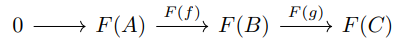
\ Finally, I will talk briefly later about Derived Functors. This advanced topic is probably best appreciated by studying Jacobson [1980] or Vakil [18 October, 2017]. I will provide a more heuristic presentation here. Consider a covariant left exact functor F : A → B between two abelian categories A and B. If 0 → A → B → C → 0 is a short exact sequence in A then applying F yields the exact sequence 0 → F(A) → F(B) → F(C) and the sequence could continue to the right to form a long exact sequence. [118] A right derived functor RiF : A → B defined for each i ≥ 1 continues the sequence as follows:
\

\ F.2.3 Applications
\ I supply one mathematical and one economic interpretation, focusing on Figure 1 in the text. The mapping idea of the Lucas critique can be viewed categorically, as the requirement for a natural transformation between the structural model and its econometric approximation in the category of sets or concrete categories, such as categories of local approximations.
\

\ This links back to the Lucas critique. We can think of the structural mapping as breaking down, when the trivial homology fails. In the next part, we will explore a particular cohomology, which is contravariant to homology, which is central to Econometric Duality. This (Principle 1) represents the deepest connection between micro-foundations, econometrics and the Lucas critique. From this standpoint, category theoretic reasoning is a cornerstone of the paper.
\
:::info This paper is available on arxiv under CC 4.0 license.
:::
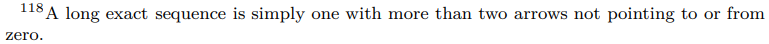
\

What's Your Reaction?









































































































