Exploring the Gradient of a Scalar in Dark Matter Velocity Analysis
This article examines the gradient of a scalar in relation to local dark matter velocity, noting a preferential direction aligned with the z-axis. By analyzing amplitude variations and deriving the marginalized likelihood, we simplify the integral through variable redefinitions, making it analytically tractable.

:::info Authors:
(1) Dorian W. P. Amaral, Department of Physics and Astronomy, Rice University and These authors contributed approximately equally to this work;
(2) Mudit Jain, Department of Physics and Astronomy, Rice University, Theoretical Particle Physics and Cosmology, King’s College London and These authors contributed approximately equally to this work;
(3) Mustafa A. Amin, Department of Physics and Astronomy, Rice University;
(4) Christopher Tunnell, Department of Physics and Astronomy, Rice University.
:::
Table of Links
2 Calculating the Stochastic Wave Vector Dark Matter Signal
3 Statistical Analysis and 3.1 Signal Likelihood
4 Application to Accelerometer Studies
4.1 Recasting Generalised Limits onto B − L Dark Matter
6 Conclusions, Acknowledgments, and References
\ A Equipartition between Longitudinal and Transverse Modes
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
D The Case of the Gradient of a Scalar
D The Case of the Gradient of a Scalar
In this case, there is a preferential direction because ∇a points in the direction of the local DM velocity. Aligning the lab’s working coordinate system such that this local velocity vector is parallel to the z axis, the amplitudes associated with the three different directions in Eq. (2.9) are not all the same. Effectively, there is an extra factor associated with the z direction, and the random signal in frequency space (c.f. Eq. (2.9)) takes the following form
\
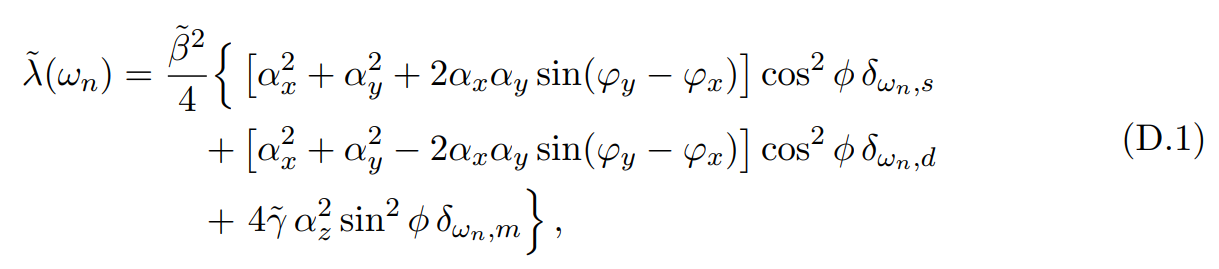
\ where (and following the notation of [45])
\
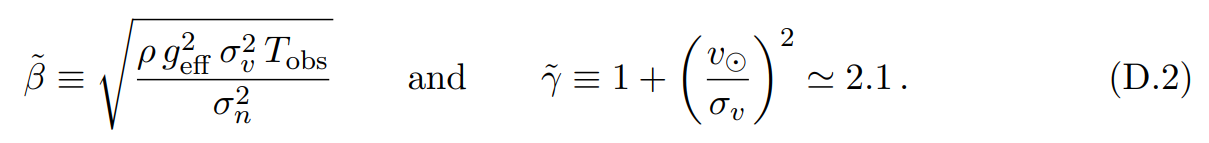
\ Proceeding similarly as in Appendix B, the marginalized likelihood is
\
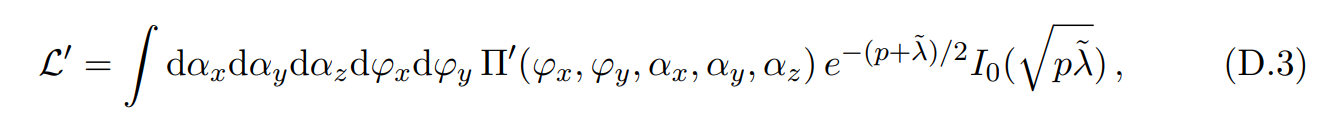
\ which we can evaluate by proceeding in the same fashion as in Appendix B; i.e. making redefinitions of the variables so they become independent and the integral becomes analytically tractable. We arrive at the following:
\
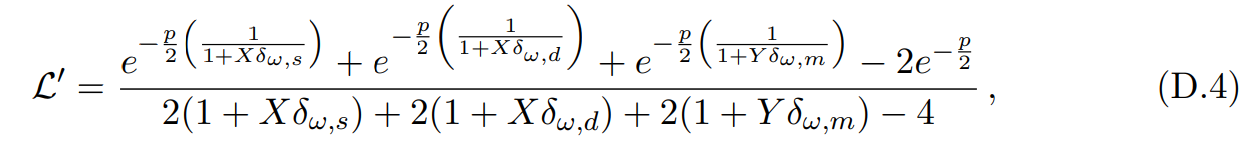
\ where
\

\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
What's Your Reaction?









































































































